What is Slope-Intercept Form of a Line? Definition and Examples

What is the slope-intercept form of a line? The slope-intercept form of a line is y  = mx + b, where m is the slope and b is the y-intercept.

How to find the slope-intercept form of a line

In order to find the slope-intercept form of a line, you may need to have one of the following situations:

• The slope and the y-intercept are given

• The graph is given

• The slope and one point on the line are given

• Two points on the line are given.

Find the slope-intercept form of a line when the slope and the y-intercept are given

Let m  = 5 and y-intercept = 2. Then, the slope-intercept form of the line is
y = 5x + 2

Find the slope-intercept form of a line when the graph is given

Use the graph of a line given below to find the slope-intercept form.

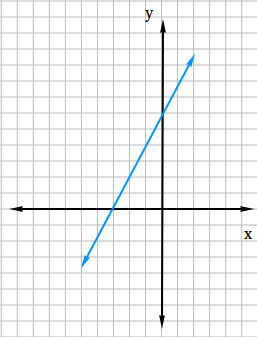
Now, show the rise and the run so you can find the slope and also the y-intercept.

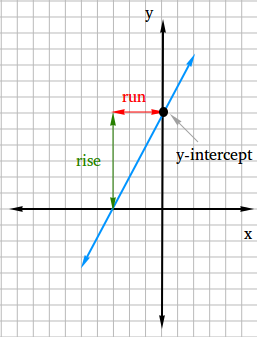
slope = rise / run = 6 / 3 = 2

y-intercept = 6

The slope-intercept form of the line is y = 2x + 6

Find the slope-intercept form of a line when the slope and one point on the line are given

Let m  = 4 and (1, -1) be a point on the line. Find the slope-intercept form of the line.

In y = mx + b, replace m with 4

y = 4x + b

Now using (1, -1), replace y with -1 and x with 1 to find b.

-1 = 4(1) + b

-1 = 4 + b

-1 - 4 = b

-5 = b

Then, the slope-intercept form of the line is y = 4x + -5

Find the slope-intercept form of a line when two points on the line are given.

Use (-4, -2) and (1, 8) to find the slope-intercept form of a line.

First, find the slope

Let (x_{1 ,} y₁) = (1, 8) and (x_{2 ,} y₂) = (-4, -2)

m = (y₁ - y₂) / x₁ - x₂) 

m =  (8 -  - 2) / 1 - -4)

m = 8 + 2 / 1 + 4

m = 10 / 5

m = 2

In y = mx + b, replace m with 2

y = 2x + b

Now using (1, 8), replace y with 8 and x with 1 to find b.

8 = 2(1) + b

8 = 2 + b

8 - 2 = b

6 = b

Then, the slope-intercept form of the line is y = 2x + 6.