What is Completing the Square? Definition and Examples

What is "completing the square"? Completing the square is the process of changing an expression like x² + bx into a perfect square trinomial by adding (b/2)² to x² + bx.

For example, you can change x² + 4x into a perfect square trinomial by adding (4/2)² or 2² = 4 to x² + 4x.

x² + 4x + 4 = (x + 2)(x + 2) = (x + 2)², so x² + 4x + 4 is a perfect square trinomial.

Completing the square using algebra tiles

Using the algebra tiles above, complete the square for x² + 4x.

First, use the algebra tiles to model x² + 4x.

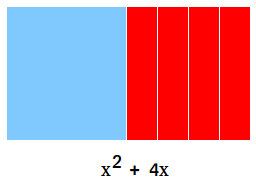
Completing the square with algebra tiles means that you will rearrange the tiles and add more tiles so that everything will look like a square. 

a. Rearrange the tiles above so that it begins to look like a square.

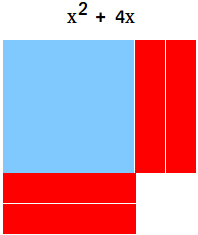
So far, you can see that it is beginning to look like a square. However, it is not a square just yet.

b. You can complete the square by adding 4 of the small green squares where you see the empty space.

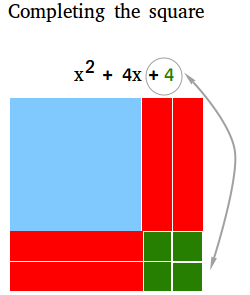
Completing the square with a couple more examples 

1. For x² + 6x + n, find the value of n that will complete the square.

n = (6/2)²

n = (3)²

n = 9

2. For x² + -8x + n, find the value of n that will complete the square.

n = (-8/2)²

n = (-4)²

n = 16