What is the common ratio of a geometric sequence?


The common ratio of a geometric sequence is the fixed number that each number in the sequence, except the first number or starting number, is multiplied by. The figure below shows the common ratio for the geometric sequence 2, 6, 18, 54, ...

Common ratio of a geometric sequence

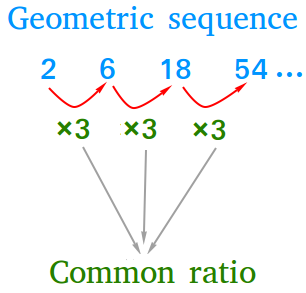
Notice that  6 / 2 = 3, 18 / 6 = 3, and 54 / 18 = 3. The name common ratio came from the fact that the ratio between consecutive numbers is constant.

Other examples showing what the common ratio of a geometric sequence is


a.

Geometric sequence: 5, 20, 80, 320, ...

The common ratio is 4

b.

Geometric sequence: 4, 20, 100, 500, ...

The common ratio is 5

c.

Geometric sequence: 4, 4r, 4r2, 4r3, ...

The common ratio is r

There is something interesting about c.!

The second number is 4r = 4r1 

The third number is 4r2 

The fourth number is 4r3 

What can we conclude about the nth number?

Notice that the exponent shown in blue is always one less than the term number (shown in red). For example, for 4r3, the exponent is 3 for the 4th number.

We can also say that for 4rn -1, the exponent is n -1 for the nth.

Therefore, nth term  = 4rn-1 for the geometric sequence 4, 4r, 4r2, 4r3, ...

Homepage

Math words beginning with the letter c

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Share this page: