Closure property


The closure property states that when you carry out a certain operation on two elements of a set, the set is closed under the operation if the result is also an element of the set.

Closure property

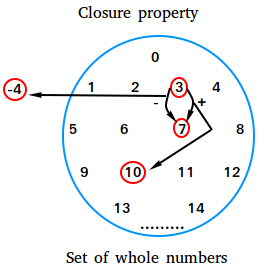
For example, as shown in the figure above, adding two whole numbers will result in a whole number. 

3 is a whole number

7 is a whole number

3 + 7 = 10 is also a whole number.

Notice that the set is the set of whole numbers

The two elements of the set are 3 and 7

The operation is addition

What can happen if the operation you carry out on 3 and 7 is subtraction instead of addition?

You could end up with a result that is not an element of the set of whole numbers.

3 - 7 = -4 

Since -4 is not a whole number, the set of whole numbers is not closed under subtraction.

More examples of the closure property

  • The set of rational numbers is closed under multiplication. In other words, if you pick any two rational numbers and multiply them, you will end up with a rational number.
  • If A and B are m × n matrices, then A + B is also an m × n matrix.
  • The set of natural numbers is closed under positive integers powers. For example, if 3 is a natural number and 2 is a positive integer, then 32 is also a natural number. 

Formal definition of the closure property

Let S be a set and * an operation. If x and y are elements of S and  x*y is also an element of S, then S is closed under the operation *

Homepage

Math words beginning with the letter c

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Share this page: